Las curvas técnicas, óvalos, ovoides y espirales, son elementos geométricos basados en las tangencias interiores de arcos.
1.- El Óvalo.
DEFINICIÓN: es una curva plana convexa y cerrada, formada por un número par de arcos de circunferencia tangentes entre sí, cuyos centros siempre están en los ejes del óvalo (que a su vez son ejes de simetría)
.
CONSTRUCCIONES:
ÓVALO CONOCIDO EL EJE DE SIMETRÍA MAYOR:
ÓVALO CONOCIDO EL EJE DE SIMETRÍA MENOR:
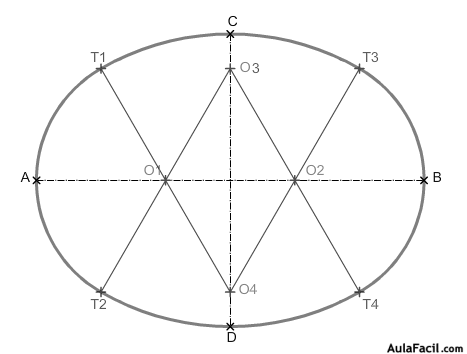
ÓVALO CONOCIDOS LOS EJES DE SIMETRÍA:
ÓVALO INSCRITO EN UN ROMBO: los ejes del óvalo están situados en las diagonales del rombo.
2.- El Ovoide.
DEFINICIÓN: es una curva plana convexa y cerrada, formada por
arcos de circunferencia tangentes entre sí. Dos de los arcos son iguales
y el resto son desiguales.
OVOIDE CONOCIDO EL EJE DE SIMETRÍA:
OVOIDE CONOCIDO EL DIÁMETRO MAYOR:
OVOIDE CONOCIDOS EL DIÁMETRO MAYOR, EL EJE MAYOR Y EL RADIO DEL ARCO MENOR:
3.- Espirales.
DEFINICIÓN: Es una curva plana, continua y abierta generada por
un punto que se desplaza alrededor de otro punto, alejándose de él a
cada vuelta.
La espiral o voluta está compuesta por arcos de circunferencia enlazados
entre sí, cuyos centros son los vértices de un polígono regular: un
triángulo equilátero, un cuadrado, ...
ESPIRAL DE DOS CENTROS: su núcleo es un segmento.
ESPIRAL DE TRES CENTROS: su núcleo es un triángulo equilátero
ESPIRAL DE CUATRO CENTROS: su núcleo normalmente es un cuadrado, pero puede ser un rectángulo.
ESPIRAL ÁUREA: está inscrita en un rectángulo áureo.
ESPIRAL DE ARQUÍMEDES: se traza a mano alzada o con plantilla.
LÁMINA DE DIBUJO:
Dibuja a escala 1:1 el capitel representado en la imagen, dimensiones en milímetros, empleando los conceptos y procedimientos de la construcción de una espiral de cuatro centros dado el paso 40, así como los conceptos y procedimientos de tangencias y enlaces del tema anterior(empieza dibujando en el centro de la lámina un segmento de 120mm, en cuyos extremos estará uno de los vertices interiores de cada cuadrado)
VOLVER
Dibuja a escala 1:1 el capitel representado en la imagen, dimensiones en milímetros, empleando los conceptos y procedimientos de la construcción de una espiral de cuatro centros dado el paso 40, así como los conceptos y procedimientos de tangencias y enlaces del tema anterior(empieza dibujando en el centro de la lámina un segmento de 120mm, en cuyos extremos estará uno de los vertices interiores de cada cuadrado)
VOLVER