1.- PROPORCIONALIDAD
En geometría la proporción se da entre segmentos y para que estos queden perfectamente definidos usamos sus vértice, por tanto, esta transformación se dibuja usando la siguiente nomenclatura: los vértices los puntos proporcionales se representan en mayúscula (las letras), sin prima para los originales (A, B, C, 1, 2...). y con prima para los transformados (A', B', C', 1', 2'...)
El Teorema de Thales es la base de la proporcionalidad entre segmentos (dividir un segmento en partes iguales).
RAZÓN: Es la relación que se establece entre las magnitudes de dos segmentos, a y b , y se representa mediante una fracción: a/b, o como una división a:b
PROPORCIONALIDAD GEOMÉTRICA: es la igualdad entre dos razones geométricas. Se representa por a/b = c/d
TERCERA PROPORCIONAL:
Cuando dos de los términos conocidos tienen el mismo
valor cualquiera de los otros recibirá el nombre de tercera
proporcional. a/b = b/x.
CUARTA PROPORCIONAL:
Cuando se conocen tres de los cuatro términos, se puede obtener el
cuarto, éste recibe el nombre de cuarta proporcional. a/b = c/x.
MEDIA PROPORCIONAL PROPORCIONAL:
Cuando se conocen solo dos de los términos. a/x = x/b
- TEOREMA DE LA ALTURA: suma de los segmentos.
- TEOREMA DEL CATETO: diferencia entre los segmentos.
.
NÚMERO AUREO
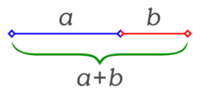
El número áureo ( = 1,618...) es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b (a más largo que b), que cumplen la siguiente relación:
= 1,618...) es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b (a más largo que b), que cumplen la siguiente relación:
- La longitud total, suma de los dos segmentos a y b, es al segmento mayor a, lo que este segmento a es al menor b. Escrito como ecuación algebraica:
SEGMENTO ÁUREO:
RECTÁNGULO ÁUREO:
Es aquél cuya proporción es tal que el lado mayor, divido por el menor da como resultado el número áureo (
2.- SEMEJANZA
Dos figuras son semejantes cuando tienen la misma forma (el mismo número de lados y ángulos iguales) y distinto tamaño (sus dimensiones son distintas).
Los diversos elementos que en las figuras semejantes se corresponden son proporcionales entre sí, existiendo igualdad entre sus ángulos.
Esta correspondencia se denomina Razón de Semejanza (K) y es la relación de proporcionalidad constante que existe entre los elementos de las dos figuras semejantes.
CONSTRUCCIÓN DE POLÍGONOS SEMEJANTES:
- EL CENTRO DE SEMEJANZA ES UN PUNTO EXTERIOR
- EL CENTRO DE SEMEJANZA ES UN VÉRTICE DE LA FIGURA:
Aplicaciones:
- Triangulos
- Polígonos conocido el lado
- Conocida la diagonal
3.- ESCALAS

TIPOS DE ESCALAS: natural, de ampliación y de reducción.
4.- TRANSFORMACIONES GEOMÉTRICAS: IGUALDAD
MÉTODOS DE CONSTRUCCIÓN DE ELEMENTOS IGUALES:
- Triangulos
- Polígonos conocido el lado
- Conocida la diagonal
3.- ESCALAS
En dibujo definimos a la escala como la proporción entre las dimensiones de un dibujo y las del objeto que representa.
Dibujar un objeto a escala es hacer una figura semejante: razón de semejanza = escala
TIPOS DE ESCALAS: natural, de ampliación y de reducción.
4.- TRANSFORMACIONES GEOMÉTRICAS: IGUALDAD
DEFINICIÓN: Dos figuras son iguales cuando al superponerlas
coinciden todos sus elementos, es decir, que los lados y los ángulos de
las dos tienen la misma forma, disposición y magnitud.
MÉTODOS DE CONSTRUCCIÓN DE ELEMENTOS IGUALES:
- Por triangulación: (Se divide la figura en triangulos y se copian)
- Por copia de ángulos:
5.- TRANSFORMACIONES GEOMÉTRICAS: TRANSLACIÓN
DEFINICIÓN: La traslación es una transformación Isométrica.
Trasladar una figura plana es aplicar a la misma un movimiento rectilíneo según una dirección dada.
Una figura transformada mediante traslación es igual al original, por tanto, sus lados son paralelos entre sí y los ángulos son iguales.
Trasladar una figura plana es aplicar a la misma un movimiento rectilíneo según una dirección dada.
Una figura transformada mediante traslación es igual al original, por tanto, sus lados son paralelos entre sí y los ángulos son iguales.
Cuando se realiza una traslación de un punto A, según vector dado v, se
transforma en otro punto A’ tal que el vector que los une AA’ = v.
TRANSLACIÓN DE UNA FIGURA:
6.- TRANSFORMACIONES GEOMÉTRICAS: GIRO
DEFINICIÓN: girar es cambiar la posición de una figura respecto
de la inicial, aplicándole un movimiento de rotación, respecto a un
punto fijo O, llamado centro de giro o de rotación. Este centro (O) de
giro puede estar situado en el interior, en el contorno o en el exterior
de la figura a transformar.
CALCULAR EL ÁNGULO Y EL VÉRTICE DE GIRO DE UNA FIGURA TRANSFORMADA:
Para calcular el ángulo y el vértice de una figura girada basta con
trazar la mediatriz a los segmentos que unen dos vértices transformados.
- Giro de una recta: sólo tienes que girar dos puntos arbitrarios de la recta. También puedes realizar el método de la siguiente animación:
- Giro de una circunferencia: sólo hay que girar su centro y trazar otra circunferencia de igual radio
7.- TRANSFORMACIONES GEOMÉTRICAS: SIMETRÍA
DEFINICIÓN: Dos
figuras son simétricas cuando todos sus elementos son iguales (igual
tamaño y forma) pero tienen distinta disposición. Las figuras simétricas
pueden estar dispuestas respecto a dos elementos: una recta (Eje de
simetría) o un punto (Vértice de simetría). Dependiendo de la
utilización de uno u otro elemento existirán dos clases de simetrías:
AXIAL y CENTRAL.
- SIMETRÍA AXIAL: Utiliza un eje de simetría. Dos figuras son simétricas respecto a un eje cuando dicho eje es la mediatriz del segmento que une los puntos que se corresponden en las dos figuras.
- SIMETRÍA CENTRAL: Los elementos están situados respecto a un punto llamado vértice de simetría. Todos sus elementos son iguales, tienen la misma forma y el mismo tamaño, pero distinta disposición.
8.- TRANSFORMACIONES GEOMÉTRICAS: HOMOTECIA
Diferencia entre homotecia y semejanza:
- La homotecia es una transformación que implica movimiento.
- La semejanza es un método constructivo que no implica movimiento.
Mediante esta transformación puedes modificar una figura, cambiando su forma y su ubicación.
DEFINICIÓN: Se llama homotecia a la transformación geométrica
que hace corresponder a un punto A otro A’, alineado con A y con otro
punto fijo O, tal que: OA’/OA = K, siendo K distinto de cero.
Al punto O se le denomina centro de homotecia, y al número K razón de la homotecia.
- Cuando K es positiva la razón se denomina directa y los puntos homotéticos estarán a un mismo lado del centro O.
- Cuando K es negativa la homotecia se denomina inversa y los puntos homotéticos estarán a distinto lado del centro O.
- Si K=1 la homotecia se transforma en identidad.
- Si K=-1 la homotecia se transforma en simetría central.
- Homotecia Directa o positiva