En este primer tema de la unidad didáctica 1 volveremos a desarrollar
conceptos y procedimientos estudiados en el curso pasado (Dibujo Técnico
I) sobre triángulos, cuadriláteros y polígonos regulares, estableciendo
nuevas relaciones entre sus elementos y aplicando la proporcionalidad y
la semejanza en su trazado, así como nuevas propiedades que se
desarrollarán más adelante.
1.- TRIÁNGULOS
En este primer apartado solamente vamos a estudiar la construcción de
triángulos escalenos, ya que los isósceles y rectángulos no presentan
dificultad alguna.
1.1.- Las rectas notables del triángulo:
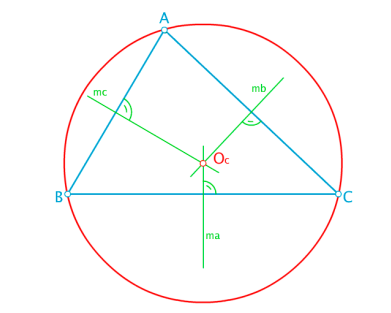
- Mediatrices y circuncentro. Las mediatrices de un triángulo son las propias mediatrices de los lados que lo conforman, las perpendiculares al lado por el punto medio. Las mediatrices de un triángulo se cortan en un punto conocido como circuncentro. Este punto es el centro de la circunferencia circunscrita la triángulo. Es decir, la circunferencia en la cual queda inscrito el triángulo.
- Bisectrices e incentro. Las bisectrices de un triángulo serán las propias bisectrices de los ángulos internos del triángulo. Estas se cortaran en un único punto conocido como incentro. Este será el centro de la circunferencia inscrita al triángulo. Es decir, la circunferencia que se encuentra dentro del triángulo y es tangente a sus tres lados
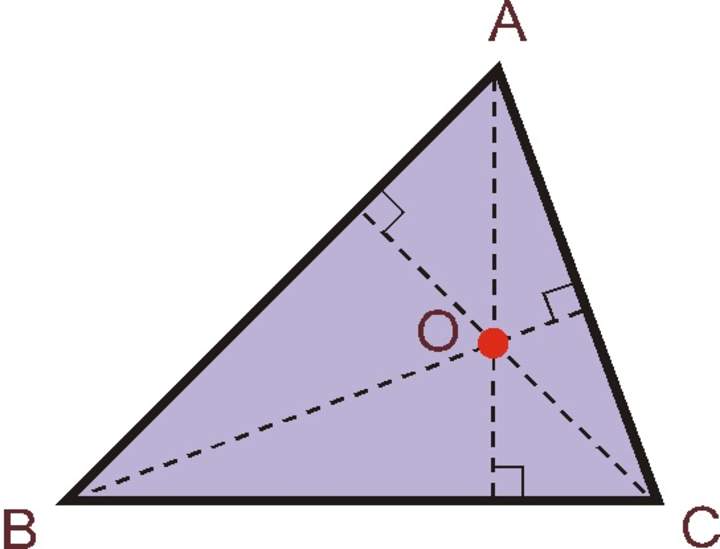
- Alturas y ortocentro. Las alturas de un triángulo son las rectas que pasando por un vértice son perpendiculares al lado opuesto o a la recta prolongación de este. El punto de corte de la altura con el lado se conoce como pie de la altura. El punto de corte de las alturas de un triángulo es el ortocentro.
- Medianas y baricentro. Las medianas son los segmentos que unen los vértices con los puntos medios de los lados opuestos. El punto de corte de las medianas de un triángulo se llama baricentro
1.2.- Triángulo interiores.
Quedan determinados por las rectas notables de un triángulo cualquiera, distinguimos tres: órtico, complementario y podar.
.
.

.
1.3.- Relación entre las rectas notables de un triángulo
- Relación entre bisectriz y mediatriz.
La intersección entre la mediatriz del lado de un triángulo y la bisectriz de su ángulo opuesto determina el circuncentro.
.
1.3.- Relación entre las rectas notables de un triángulo
- Relación entre bisectriz y mediatriz.
La intersección entre la mediatriz del lado de un triángulo y la bisectriz de su ángulo opuesto determina el circuncentro.
-Relación entre las medianas.
Recordemos las dos principales características de una mediana y su baricentro, respecto del vértice y del lado:
- La distancia al vértice corresponde a 2/3 de la longitud total de la mediana.
- La distancia al punto medio del lado corresponde a 1/3 de la longitud total de la mediana.
ACTIVIDAD:
1.4.- Construcción de triángulos usando el arco capaz
- Definición de arco capaz:
Recordemos que el arco capaz es lugar geométrico de todos los puntos del plano desde los cuales se observa un segmento bajo un mismo ángulo.
Ejemplo:
Todos los puntos del arco formarán un triángulo con el segmento base con un ángulo constante de 60º
- Cálculo del arco capaz de un segmento dado el ángulo.
Simplemente hay que llevar al extremo del segmento el valor 90º- (ángulo dado) , y donde corte a la mediatriz del segmento será el centro del arco capaz (y será el centro del circuncentro del triangulo formado)
- Construcción de un triángulo dada la altura ,ángulo de un vertice y la longitud del lado opuesto.
Calculamos CC a través de la mediatriz (Mc) y el ángulo conocido (90-ángulo) , y con el arco capaz y la altura obtenemos C.
- Construcción de un triángulo dada la base, el ángulo opuesto y su mediana.
Calculamos CC a través de la mediatriz (Mc) y el ángulo conocido (90-ángulo) , y con el arco capaz y la mediana obtenemos C.
1.5.- Construcción de un triangulo semejante
- Usando la Mediana: La mediana semejante tendrá la misma posición que la auxiliar , solo variará su tamaño
Ejemplo:
- Usando la bisectriz: Como en el caso anterior, la bisectriz conocida tendrá la misma disposición que la auxiliar, por tanto, procederemos de la misma manera.
Ejemplo: .
Actividad:
Construcción de un triángulo escaleno conocida la posición de un vértice A, su ángulo Aº, su altura y el valor de otro ángulo Cº.
En la resolución de este ejercicio hemos aplicado semejanza.
APUNTES: POLÍGONOS Y CONSTRUCCIÓN DE TRIÁNGULOS
APUNTES 2: CUADRILÁTEROS Y POLÍGONOS REGULARES